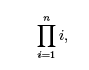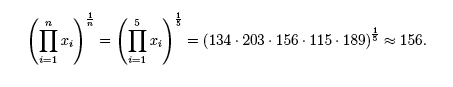Mathematical Notation
Summation Notation
|
You will often encounter summation notation when you look at, or perform, statistical analysis of biological data. Imagine that you are performing a simple experiment: comparing the weight of a two populations of mice, one that was fed a high fat diet and a control group on a normal diet. The graduate student you are working with says that you can calculate the average or mean weight of each population as follows:
What does that notation actually say? To understand it, you must know how to read summation notation.
We will focus solely on understanding summation notation. For the life sciences, it is more important to be able to take a summation notation that has been given to you and know what it means than it is to express a given sum in summation notation. Summation notation is used to compactly represent a sum of numbers. For example, suppose we want to compactly write the following sum, 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15. Sums of numbers, such as the one above, are often called series. To compactly write the above series, we use the following summation notation,
To understand how this notation represents the above sum, we break the summation notation down into pieces:
The terms we are going to be summing usually depend on the index of the sum. That is, as the index increments from the lower limit to the upper limit, the terms in the series usually change. In this case, we are summing the first 15 numbers, so the index itself represents the numbers we are summing. Consider the following summation notation, where the parentheses make it clear that both terms are part of the sum. In this case, the index (i) begins at 0 and ends at 4. We can write out the terms in the summation as i increases from 0 to 4 by substituting each value of i, and then summing the numbers as follows,
(5+2 ·0)+(5+2 ·1)+(5+2 ·2)+(5+2 ·3)+(5+2 ·4) = 5+7+9+11+13 = 45. Another example involving summation notation is given by, We can take this compact notation and write out the terms in the sum as, (12−1)+(22−1)+(32−1)+(42−1)+(52−1)+(62−1) = 0+3+8+15+24+35 = 85. The sums we have looked at so far are finite sums with finite upper and lower limits. Sums can also be infinite (e.g., the upper index equals ∞). For example, the sum given by,
means to sum an infinite number of terms as,
The value of an infinite sum may be ∞ (in this case the sum is infinite). This is a more delicate topic that will be discussed in a later section. Using summation notation to represent the arithmetic mean. We can also use summation notation to represent the arithmetic mean or average
we can express the mean as,
Now try some problems that test your knowledge of mathematical notation. |
The Biology Project > Biomath > Notation > Summation
Department of Biochemistry and Molecular Biophysics
The University of Arizona
February 2006
Contact the Development Team
http://www.biology.arizona.edu
All contents copyright © 2006. All rights reserved.
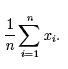
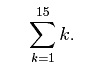
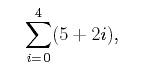
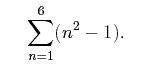
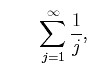


![mean = 1/5(134 + 203+156+115+189] = 797/5 =159](images/meanexample.gif)