We will discuss two types of reflections: reflections across the x-axis and reflections across the y-axis.

Reflections Across the x-Axis

To visualize a reflection across the x-axis, imagine the graph that would result from folding the base graph along the x-axis. Symbolically, we define reflections across the x-axis as follows:

In other words, all of the portions of the graph above the x-axis will be reflected to the corresponding position below the x-axis, while all of the portions of the graph below the x-axis will be reflected above the x-axis. Of course, x-intercepts will remain unchanged under this type of reflection

Examples of Reflections Across the x-Axis

Consider the following base functions,

(1) f (x) = x² - 9,

(2) g(x) = | x | + 1 .

The graphical representation of function (1), f (x), is a parabola shifted 9 units down with respect to the base function y = x². What do you suppose the graph of

y₁(x) = -f (x)

looks like? Using the definition of f (x), we can write y₁(x) as,

y₁(x) = -f (x) = -(x²-9) = -x² + 9.

Based on the definition of reflection across the x-axis, the graph of y₁(x) should look like the graph of f (x), reflected across the x-axis. Take a look at the graphs of f (x) and y₁(x).

Function (2), g(x), is an absolute value function. What would the graph of

y₂(x) = -g(x)

look like? Using our knowledge of reflections across the x-axis, the graph of y₂(x) should look like the base graph g(x) reflected across the x-axis. To check this, we can write y₂(x) as,

y₂(x) = -g(x) = -(|x| + 1) = - |x| -1 ,

construct a table of values, and plot the graph of the new function. As you can see, the graph of y₂(x) is in fact the base graph g(x) reflected across the x-axis.

Reflections Across the y-Axis

You can visualize a reflection across the y-axis by imagining the graph that would result from folding the base graph along the y-axis. Symbolically, we define reflections across the y-axis as follows:

In other words, all of the portions of the graph to the left of the y-axis will be reflected to the corresponding position to the right of the y-axis, while all of the portions of the graph to the right of y-axis will be reflected to the corresponding positions to the left of the y-axis. Of course, y-intercepts will remain unchanged under this type of reflection.

Examples of Reflections Across the y-Axis

Consider the following base functions,

(1) f (x) = (x-1)² ,

(2) g(x) = x³ - x² - 4x + 4.

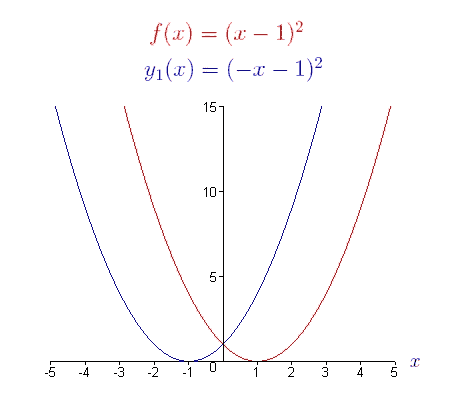
The graphical representation of function (1), f (x), is a parabola shifted 1 unit to the right. What do you suppose the graph of

y₁(x) = f (-x)

looks like? Using the definition of f (x), we can write y₁(x) as,

y₁(x) = f (-x) = (-x -1)² = x² + 2x +1 .

Based on the definition of reflection across the y-axis, the graph of y₁(x) should look like the graph of f (x), reflected across the y-axis. Take a look at the graphs of f (x) and y₁(x).

Function (2), g(x), is a cubic function. What would the graph of

y₂(x) = g(-x)

look like? Using our knowledge of reflections across the y-axis, the graph of y₂(x) should look like the base graph g(x) reflected across the y-axis. To check this, we can write y₂(x) as,

y₂(x) = g(-x) = (-x)³ - (-x)² -4(-x) + 4 = -x³ + x² + 4x + 4,

construct a table of values, and plot the graph of the new function. As you can see, the graph of y₂(x) is in fact the base graph g(x) reflected across the y-axis.

*****

Now try some problems that test your knowledge of graphical transformations

Problems