Polynomial Functions
Basics
|
Definition A polynomial in the variable x is a function that can be written in the form, where an, an-1 , ..., a2, a1, a0 are constants. We call the term containing the highest power of x (i.e. anxn) the leading term, and we call an the leading coefficient. The degree of the polynomial is the power of x in the leading term. We have already seen degree 0, 1, and 2 polynomials which were the constant, linear, and quadratic functions, respectively. Degree 3, 4, and 5 polynomials also have special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called nth degree polynomials. The names of different polynomial functions are summarized in the table below.
Some examples of polynomials include:
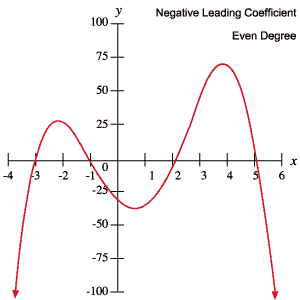
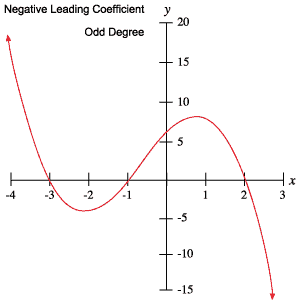
The Limiting Behavior of Polynomials The limiting behavior of a function describes what happens to the function as x → ±∞. The degree of a polynomial and the sign of its leading coefficient dictates its limiting behavior. In particular,
These results are summarized in the table below.
The following graphs of polynomials exemplify each of the behaviors outlined in the above table.
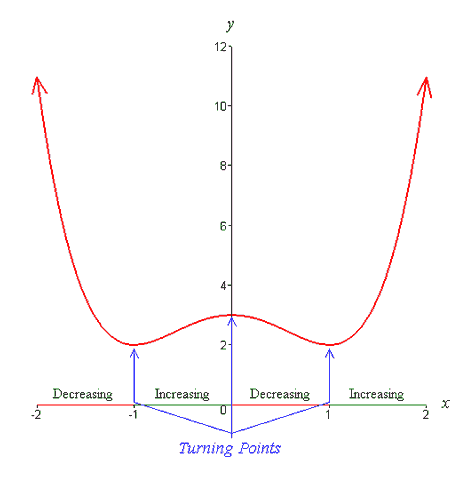
Roots and Turning Points The degree of a polynomial tells you even more about it than the limiting behavior. Specifically, an nth degree polynomial can have at most n real roots (x-intercepts or zeros) counting multiplicities. For example, suppose we are looking at a 6th degree polynomial that has 4 distinct roots. If two of the four roots have multiplicity 2 and the other 2 have multiplicity 1, we know that there are no other roots because we have accounted for all 6 roots. This is because the roots with a multiplicity of two (also known as double roots) are counted as two roots. Be aware that an nth degree polynomial need not have n real roots — it could have less because it has imaginary roots. Notice that an odd degree polynomial must have at least one real root since the function approaches - ∞ at one end and + ∞ at the other; a continuous function that switches from negative to positive must intersect the x- axis somewhere in between. In addition, an nth degree polynomial can have at most n - 1 turning points. A turning point is a point at which the function changes from increasing to decreasing or decreasing to increasing as seen in the figure below. Again, an nth degree polynomial need not have n - 1 turning points, it could have less.
Domain and Range All polynomials have the same domain which consists of all real numbers. The range of odd degree polynomials also consists of all real numbers. The range of even degree polynomials is a bit more complicated and we cannot explicitly state the range of all even degree polynomials. If the leading coefficient is positive the function will extend to + ∞; whereas if the leading coefficient is negative, it will extend to - ∞. This means that even degree polynomials with positive leading coefficient have range [ymin, ∞) where ymin denotes the global minimum the function attains. On the other hand, even degree polynomials with negative leading coefficient. have range (-∞, ymax] where ymax denotes the global maximum the function attains. In general, it is not possible to analytically determine the maxima or minima of polynomials. ***** In the next section you will learn polynomial division, a technique used to find the roots of polynomial functions. | |||||||||||||||||||||||||||||
The Biology Project > Biomath > Polynomial Functions > Basics
Department of Biochemistry and Molecular Biophysics
The University of Arizona
March 2006
Contact the Development Team
http://www.biology.arizona.edu All contents copyright © 2006. All rights reserved.

 You can use this information to determine whether or not a polynomial has odd or even degree and whether the leading coefficient is positive or negative, simply by inspecting its graph.
You can use this information to determine whether or not a polynomial has odd or even degree and whether the leading coefficient is positive or negative, simply by inspecting its graph.