|
Logarithms are encountered throughout the biological sciences. Some examples
include calculating the pH of a solution or the change in free energy
associated with a biochemical reactions. To understand how to solve these
equations, we must first consider the definition of a logarithm.
Definition
The formal definition of a logarithm is as follows:
the base a logarithm
of a positive number x is the exponent you
get when you write x as
a power of a where a > 0 and a ≠ 1.
That is,
loga x = k if
and only if a k = x
The key to taking
the logarithm of x > 0 is to rewrite x using
base a. For example,
log2 32 = 5
can be rewritten as
2 5 = 32
As you work the examples in this section, notice the outputs of logarithms
increase linearly as the inputs increase exponentially. Like
scientific notation (link to section), logarithms are used to simplify
calculations with large numbers.
Examples
Logarithms, just like exponents, can have different bases. In the biological
sciences, you are likely to encounter the base 10 logarithm, known as
the common logarithm and denoted simply as log; and the base e logarithm,
known as the natural log and denoted as ln. Most calculators will easily
compute these widely used logarithms.
Base 10 logarithm
The common logarithm of a positive number x,
is the exponent you get when
you write x as a power of
10. That is,
log x = k if
and only if 10 k = x
Computing the common logarithm of x > 0 by hand can only be done under
special circumstances,
and we will examine these first. Let’s begin with computing
the value of,
log 10.
According to our definition of the common logarithm, we need to rewrite
x = 10 using base
10. This is easy to do because 10 = 101. So the exponent, k, we get
when rewriting 10 using
base 10 is, k = 1. Thus, we conclude,
log 10 = log 101 = 1.
While this example is rather simple, it is good practice
to follow this method of solution. Now
try the following exercises.
Test yourself with the following exercises
Natural logarithms
The natural logarithm of a positive number x,
is the exponent you get when you write x as
a power of e. Recall that
loge x =
ln x
therefore
ln x = k if
and only if e k = x
Calculations with logarithms in
other bases.
Now, suppose you were asked to compute the value of log 20. What would you
do (or try to do) to get an answer? Do you notice anything different about
this problem?
As you most likely noticed, there is no integer k, such that 10k =
20. So, in this case, you will need to rely on your calculator for help.
Using your calculator you will find,
log 20 ≈ 1.30.
Remember that this is true because,
101.30 ≈ 20.
Again, test yourself
After completing these exercises you will notice that your
answers (outputs) are small relative to your large inputs. Remember
that logarithms transform exponentially increasing inputs into
linearly increasing outputs. This is quite convenient for biologists
who work over many orders of magnitude and on many different
scales.
Inverses
Since exponential and logarithmic functions are inverses, the
domain of logarithms is the range
of exponentials (i.e. positive real numbers), and the range
of logarithms is the domain of
exponentials (i.e. all real numbers). This is true of all logarithms,
regardless of base.
Recall
that an exponential function with base a is
written as f (x) = a x. The inverse of this
function is a base a logarithmic function written as,
f −1 (x)
= g (x) = loga x.
When there is no explicit subscript a written,
the logarithm is assumed to be common (i.e.
base 10). There is one special exception to this notation
for base e ≈ 2.718, called the natural logarithm,
g (x) = loge x = ln x.
To compute the base a logarithm of x > 0,
rewrite x using
base a (just as we did for
base 10). For example, suppose a =
2 and we want to compute,
log2 8.
To find this value by hand, we convert the number 8 using
base 2 as,
log2 8 = log2 23 = 3,
just as we did for base 10.
Using this methodology, test yourself
by computing the following by hand.
Properties of Logarithms
Understanding the properties of logarithms will help you solve
equations involving exponentials and logarithms. Recall that
the formal definition of a logarithm is
loga x = k if
and only if a k = x
where a, the base of the logarithm, is greater
than zero and not equal to 1 and x is
a positive number.
Logarithms have the following properties
|
1.
|
loga a x = x for
any real number x,
|
|
2.
|
aloga x =
x for any positive number x.
For positive real numbers m, n,
and any real number r, and a > 0 and a ≠ 1, |
|
3.
|
loga 1 = 0,
|
|
4.
|
loga m + loga n =
loga (mn),
|
|
5.
|
loga m − loga n =
loga (m/n) ,
|
|
6.
|
loga (mr )
= r loga m. |
Changing the base of a logarithm
Once you have simplified a logarithmic equation using the definition
and properties of logarithms, you will need to calculate the
answer. Some calculators will only compute common logarithms
and natural logarithms (a =
10 and a = e,
respectively). In these cases you will need change the base.
The change of base formula is given by,
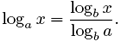
For calculator convenience, we usually select b to
be 10 or e.
For example, log4 73
can be computed as
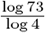
or as
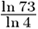
in your calculator.
Using your calculator and the change of base formula, test yourself.
It is also important to realize that to graph
the function y =
loga x, where a ≠ 10
and a ≠ e, in your calculator, you
will need to input this function as,
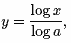
or as,
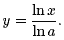
*****
In the next section we will begin an exploration of the
graphs of logarithmic functions. Introduction | Graphing |