Quadratic Functions
Solving Quadratic Equations
|
A quadratic equation is an equation that can be written in the form, ax2 + bx + c = 0. Notice that we solve this same equation to find the roots of a quadratic function. To solve a quadratic equation means to find the values of x such that the above equation holds true. You can solve quadratic equations by completing the square, using the quadratic formula, or, in rare cases, by factoring. We will discuss factoring at the end of this section. In most cases, solving quadratic equations is most easily accomplished using the quadratic formula. We will now look at some examples. Example 1: Solving Quadratic Equations Suppose you were asked to solve the equation, −4x2 + x + 9 = 6. To use the quadratic formula, we must get this equation in the form ax2 + bx + c = 0 as, −4x2 + x + 3 = 0. We now find the solutions using the quadratic formula as, which yields the two solutions,
Therefore, we conclude that the equation −4x2 + x + 9 = 6 has two solutions, x = −3/4 and x = 1. Example 2: Solving Quadratic Equations In some cases, using the quadratic formula is not necessary to solve a quadratic equation. Consider the following equations, 18x − 3x2 = 0, 4x2− 9 = 0. Notice that the first equation has no constant term on the left hand side, and the second equation has no x term on the left hand side. Thus, we can solve these equations without the quadratic formula. To solve the first equation, 18x − 3x2 = 0, we factor out 3x as, 18x − 3x2 = 3x(6 − x) = 0. We can now use the fact that if 3x(6 − x) = 0, then either 3x = 0 or 6 − x = 0. The equation 3x = 0 implies x = 0. The equation 6−x = 0 implies x = 6. Thus, we have the two solutions x = 0 and x = 6. Be sure not to make the following mistake when solving this equation,
Notice that by canceling x on the both sides of the equation, we have lost the solution x = 0. Keep in mind that canceling x is the same thing as dividing through by x on both sides. Remember that division by x is only valid for x≠ 0 because division by zero is undefined. To solve the second equation, 4x2− 9 = 0, we have, When taking the square root of both sides of the above equation, be sure to include both the positive and the negative roots. Solving Quadratic Equations by Factoring In some cases, you can solve a quadratic equation by factoring. For example, consider the following equation, x2− 6x + 8 = 0. This equation can be solved by factoring. In particular, −4 and −2 add to −6 (the coefficient of x) and multiply to 8 (the constant term). Thus, we can factor the equation x2− 6x + 8 = 0 as, (x − 4)(x − 2) = 0. Now we use the fact that if (x − 4)(x − 2) = 0, then either x − 4 = 0 or x − 2 = 0. Thus, we have the solutions x = 4 and x = 2. Factoring should only be used when you can quickly identify the factored form. Factoring is much more complicated when the leading coefficient is not 1. If this is the case
***** Now try some problems that involve quadratic functions. |
The Biology Project > Biomath > Quadratic Functions> Solving Quadratic Equations
Department of Biochemistry and Molecular Biophysics
The University of Arizona
January 2006
Contact the Development Team
http://www.biology.arizona.edu
All contents copyright © 2006. All rights reserved.


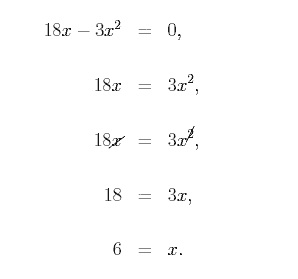

 Remember, you can always use the quadratic formula to find solutions.
Remember, you can always use the quadratic formula to find solutions.