The laws of exponents are a set of five rules that show us how
to perform some basic operations using exponents.
Mathematically
they are defined as follows:
Let a and b be real
numbers and m and n be positive integers. Then the following laws
hold:

Notice that we have taken our exponents to be positive integers.
This is the most intuitive
choice because we know that,
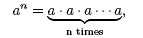
where n is a positive integer. We can also use the first
law of exponents to define the zero and negative exponents,

In (1), a 0 behaves like the
number 1, and we define a 0 = 1. In
(2), a −n behaves like the
reciprocal of a n and we write,

The laws of exponents provide a set of rules
that can be used to simplify complex expressions that contain
exponents.
These rules are important when simplifying expressions
involving exponents. For example, we
can use laws of exponents to make the following simplification,
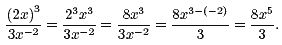
The purpose of simplification will become evident as you begin
to solve problems involving
exponents; sometimes these simplifications are necessary to see
the next step in solving a
problem.
 A common mistake you should avoid
A common mistake you should avoid
It is important to recognize when no simplification
can be made. Notice that
the laws of exponents do not involve sums or differences of
terms with exponents.
You might be tempted to write,
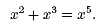
However, this statement is incorrect because the
sum of two exponents cannot be further simplified. Many of the applications we discuss will require that you simplify an expression that contains exponents. When doing so, you must keep in mind the rules we have
described in this section.
*****

