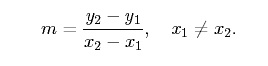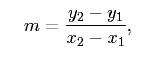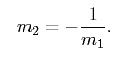Linear Functions
Exploring the Concept of Slope
|
Slope-Intercept Form Linear functions are graphically represented by lines and symbolically written in slope-intercept form as, y = mx + b, where m is the slope of the line, and b is the y-intercept. We call b the y-intercept because the graph of y = mx + b intersects the y-axis at the point (0, b). We can verify this by substituting x = 0 into the equation as, y = m · 0 + b = b. Notice that we substitute x = 0 to determine where a function intersects the y-axis because the x-coordinate of a point lying on the y-axis must be zero. The Definition of Slope : The constant m expressed in the slope-intercept form of a line, y = mx + b, is the slope of the line. Slope is defined as the ratio of the rise of the line (i.e. how much the line rises vertically) to the run of line (i.e. how much the line runs horizontally).
Intuitively, we can think of the slope as measuring the steepness of a line. The slope of a line can be positive, negative, zero, or undefined. A horizontal line has slope zero since it does not rise vertically (i.e. y1 − y2 = 0), while a vertical line has undefined slope since it does not run horizontally (i.e. x1 − x2 = 0). Zero and Undefined Slope As stated above, horizontal lines have slope equal to zero. This does not mean that horizontal lines have no slope. Since m = 0 in the case of horizontal lines, they are symbolically represented by the equation, y = b. Functions represented by horizontal lines are often called constant functions. Vertical lines have undefined slope. Since any two points on a vertical line have the same x-coordinate, slope cannot be computed as a finite number according to the formula,
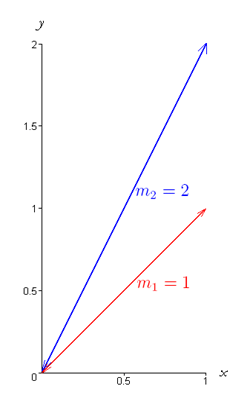
because division by zero is an undefined operation. Vertical lines are symbolically represented by the equation, x = a where a is the x-intercept. Vertical lines are not functions; they do not pass the vertical line test at the point x = a. Positive Slopes Lines in slope-intercept form with m > 0 have positive slope. This means for each unit increase in x, there is a corresponding m unit increase in y (i.e. the line rises by m units). Lines with positive slope rise to the right on a graph as shown in the following picture,
Lines with greater slopes rise more steeply. For a one unit increment in x, a line
with slope
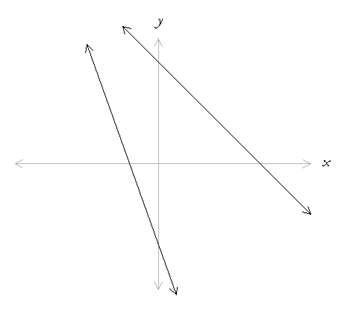
Negative Slopes Lines in slope-intercept form with m < 0 have negative slope. This means for each unit increase in x, there is a corresponding |m| unit decrease in y (i.e. the line falls by |m| units). Lines with negative slope fall to the right on a graph as shown in the following picture,
The steepness of lines with negative slope can also be compared. Specifically, if two lines have negative slope, the line whose slope has greatest magnitude (known as the absolute value) falls more steeply. For a one unit increment in x, a line with slope m3 = −1 falls one unit while a line with slope m4= −2 falls two units as depicted,
Parallel and Perpendicular Lines Two lines in the xy-plane may be classified as parallel or perpendicular based on their slope. Parallel and perpendicular lines have very special geometric arrangements; most pairs of lines are neither parallel nor perpendicular. Parallel lines have the same slope. For example, the lines given by the equations, y1 = −3x + 1, y2 = −3x − 4, are parallel to one another. These two lines have different y-intercepts and will therefore never intersect one another since they are changing at the same rate (both lines fall 3 units for each unit increase in x). The graphs of y1 and y2 are provided below,
Perpendicular lines have slopes that are negative reciprocals of one another. In other words, if a line has slope m1, a line that is perpendicular to it will have slope,
An example of two lines that are perpendicular is given by the following, These two lines intersect one another and form ninety degree (90°) angles at the point of intersection. The graphs of y3 and y4 are provided below,
In the next section we will describe how to solve linear equations. |
The Biology Project > Biomath > Linear Functions > Concept of Slope
The Biology Project
Department
of Biochemistry and Molecular Biophysics
The University of Arizona
January 2006
Contact the Development Team
http://www.biology.arizona.edu
All contents copyright © 2006. All rights reserved.