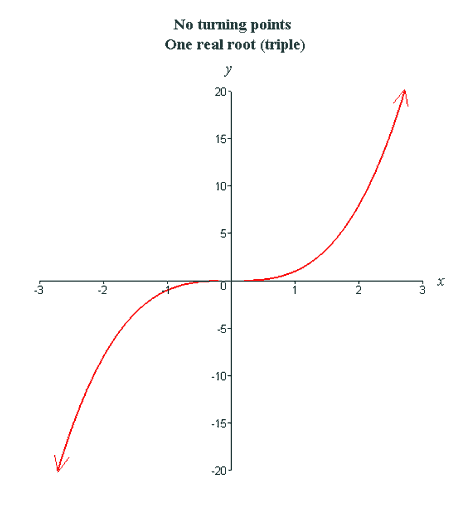
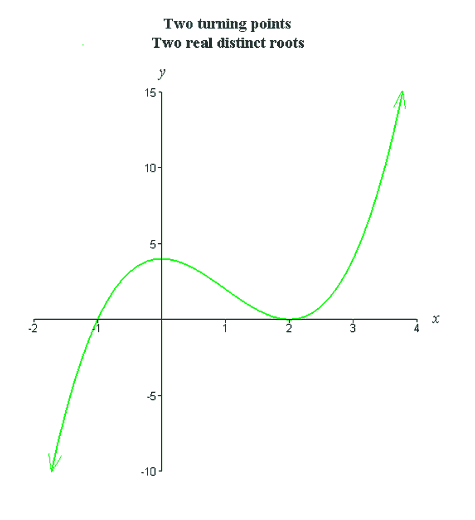
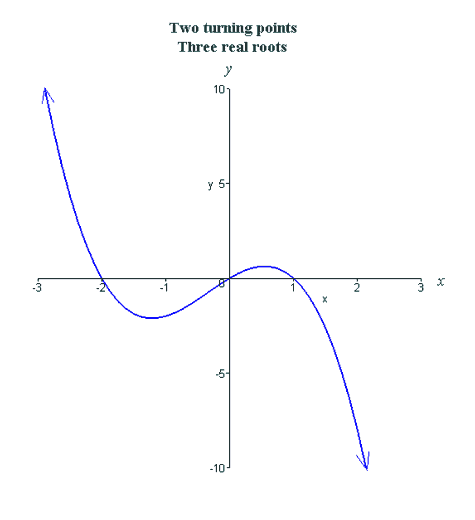
In this section we will explore the graphs of polynomials. We have already discussed the limiting behavior of even and odd degree polynomials with positive and negative leading coefficients. Also recall that an n^th degree polynomial can have at most n real roots (including multiplicities) and n−1 turning points. We will explore these ideas by looking at the graphs of various polynomials.

Cubic functions can have at most 3 real roots (including multiplicities) and 2 turning points. We will look at the graphs of cubic functions with various combinations of roots and turning points as pictured below.

The multiplicity of a root affects the shape of the graph of a polynomial. Specifically,

• If a root of a polynomial has odd multiplicity, the graph will cross the x-axis at the the root.
• If a root of a polynomial has even multiplicity, the graph will touch the x-axis at the root but will not cross the x-axis.

As the multiplicity of the root increases, the graph flattens out more and more near the root. In the red graph above, there is one distinct real root, x = 0, having multiplicity 3. Since the multiplicity is odd, the graph does cross the x-axis at the root, but the graph flattens out near this root because the root is not simple. In the green graph above, there are two distinct real roots, x₁ = −1 and x₂ = 2. Notice that the graph does not cross the x-axis at the root x₂ = 2 (it simply touches the x-axis). This indicates that x₂ = 2 is a root of even multiplicity (in fact, the multiplicity is 2 because a cubic is only degree 3). Thus, the cubic pictured in green has one simple root, x = −1, and one double root, x = 2 (for a total, including multiplicities, of 3).

We can actually take a look at how increasing multiplicity affects the shape of the graph near a root. The figure below shows polynomials with one distinct real root, x = 0. As you can see, the graph touches the root without crossing the x-axis when the multiplicity is even, and crosses the x-axis through the root when the multiplicity is odd. Furthermore, the graph flattens out more and more near the root as the multiplicity increases.

*****

Now try some problems that will test your knowledge of polynomial functions.

Problems